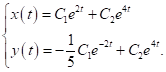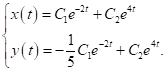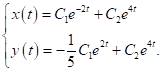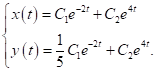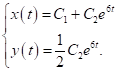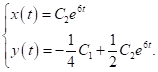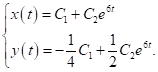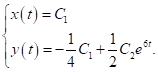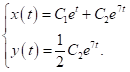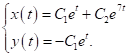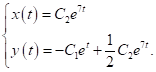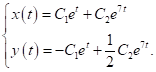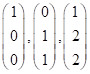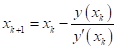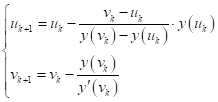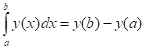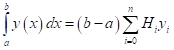Тема :: Диференціальні рівняння
- рівняння, яке містить незалежну змінну, невідому функцію та її першу похідну
- рівняння, яке містить незалежну змінну, невідому функцію та її першу і другу похідну
- рівняння, яке містить незалежну змінну, невідому функцію
- правильної відповіді немає
- таку пару чисел, яка при підстановці в рівняння перетворює його в тотожність при всіх аргументах з цього інтервалу
- недиференційовну на цьому інтервалі функцію, яка при підстановці в рівняння перетворює його в тотожність при всіх аргументах з цього інтервалу
- диференційовну на цьому інтервалі функцію, яка при підстановці в рівняння перетворює його в тотожність при всіх аргументах з цього інтервалу
- правильної відповіді немає
- рівнянням Бернуллі
- рівнянням Бореллі
- рівнянням да Вінчі
- рівнянням Торічеллі
- рівняння, що пов’язує незалежну змінну, невідому функцію та першу і другу похідні цієї функції
- рівняння Бернуллі
- рівняння, що пов’язує незалежну змінну, квадрат невідомої функції та першу похідну цієї функції
- правильної відповіді немає
- лінійним однорідним диференціальним рівнянням першого порядку
- рівнянням Бернуллі
- лінійним однорідним диференціальним рівнянням другого порядку
- лінійним неоднорідним диференціальним рівнянням другого порядку
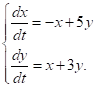 має вигляд
має вигляд
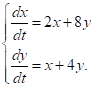 має вигляд
має вигляд
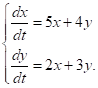 має вигляд
має вигляд
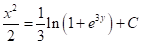
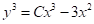
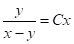
- правильної відповіді немає
Тема :: Теорія ймовірностей
- 0,1
- 0,25
- 0,5
- 0,75
- 0,5
- 0,9
- 0,75
- 0,976
- 1/9
- 1/2
- 1/3
- 1/6
- 3/4
- 5/6
- 11/18
- 7/9
- 0
- 1
- 2
- 3
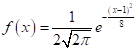 , а величина Y розподілена рівномірно на [0; 2]. Обчислити величину: M(5XY+1)+D(3X–2).
, а величина Y розподілена рівномірно на [0; 2]. Обчислити величину: M(5XY+1)+D(3X–2).
- 10
- 20
- 42
- 50
- простір елементарних подій містить скінченну кількість елементарних подій
- можна описати множину можливих результатів
- простір елементарних подій складається зі скінченної кількості рівноможливих результатів
- усі сприятливі події є рівноможливими
- ймовірності суми несумісних подій
- ймовірності суми незалежних подій
- ймовірності суми залежних подій
- ймовірності суми сумісних подій
- ймовірності добутку несумісних подій
- ймовірності добутку незалежних подій
- ймовірності добутку залежних подій
- ймовірності добутку сумісних подій
- ймовірності суми незалежних подій
- ймовірності суми залежних подій
- ймовірності суми несумісних подій
- ймовірності суми сумісних подій
- P(A)*P(B)
- P(A|B)*P(B|A)
- (1 – P(A))*(1 – P(B))
- P(B)*P(A|B)
- P(AB)/P(B)
- P(A)*P(AB)
- P(B)/P(AB)
- P(AB)*P(B)
- P(A)*P(B)
- 1 – (1 – P(A))*(1 – P(B))
- 1 – P(A)*P(B)
- (1 – (P(A))*(1 – P(B))
- P(A)*P(B)
- 1 – P(A)*P(B)
- (1 – (P(A))*(1 – P(B))
- 1 – (1 – P(A))*(1 – P(B))
- P(A) + P(B) + P(C)
- (1 – P(A))*(1 – P(B))*(1 - P(C))
- 1 – P(A)*P(B)*P(C)
- P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC)
- функція розподілу X
- щільності розподілу X
- математичне сподівання X
- характеристична функція
- функція розподілу X
- щільності розподілу X
- математичне сподівання X
- характеристична функція
- 0,68
- 0,95
- 0,99
- 0,59
- помножиться на 4
- помножиться на 1/2
- поділиться на 2
- помножиться на 2
- помножиться на 2
- помножиться на 1/2
- помножиться на 4
- поділиться на 2
- помножиться на 2
- помножиться на 4
- помножиться на 1/2
- поділиться на 2
- Гауса
- Бернуллі
- Муавра – Лапласа
- Байєса
- Гауса
- Бернуллі
- Муавра – Лапласа
- Байєса
- повні ймовірності
- апріорні ймовірності гіпотез
- апостеріорні ймовірності гіпотез
- ймовірності незалежних подій
- рівномірний
- Стьюдента
- Гауса
- Бернуллі
- 0,4
- 0,5
- 0,55
- 0,6
- 1/4
- 1/20
- 1/25
- 1/30
- 0,425
- 0,325
- 0,575
- 0,650
- (1-0,99)*(1-0,99)*(1-0,99)
- 1- 0,01*0,01*0,01
- 1-0,99*0,99*0,99
- 3*0,01*0,99
- 0,123
- 0,325
- 0,243
- 0,432
- 0,14
- 0,26
- 0,38
- 0,42
- 0,2
- 0,3
- 0,4
- 0,5
- 0,75
- 0,5
- 0,25
- 0,125
- 0,25
- 0,35
- 0,65
- 0,75
- f(x) = 0, якщо x <= 0, f(x) = x^2/2, якщо 0 < x <=2, f(x) = 0, якщо x > 2
- f(x) = 0, якщо x <= 0, f(x) = x^2/4, якщо 0 < x <=2, f(x) = 1, якщо x > 2
- f(x) = 0, якщо x <= 0, f(x) = 1/2, якщо 0 < x <=2, f(x) = 0, якщо x > 2
- f(x) = 0, якщо x <= 0, f(x) = 1/2, якщо 0 < x <=2, f(x) = 1, якщо x > 2
Тема :: Математична статистика
- середнє
- медіана
- дисперсія
- коефіцієнт варіації
- середньоквадратичне відхилення
- 99
- 94
- 90
- 100
- обидві гіпотези (нульова та альтернативна) невірні;
- обидві гіпотези вірні;
- буде помилково прийнята альтернативна гіпотеза, якщо вірна нульова;
- буде помилкова прийнята нульова гіпотеза, якщо вірна альтернативна;
- одна з гіпотез невірна, але невідомо яка.
- вірна нульова гіпотеза;
- вірна альтернативна гіпотеза;
- жодна гіпотеза невірна;
- немає підстав відкинути нульову гіпотезу, що, однак, не свідчить про її справедливість
- середнє арифметичне
- медіана
- мода
- бісектриса
- дисперсія
- медіана
- мода
- хорда
- при зростання надійності точність підвищується
- при зростання надійності точність понижується
- точність та надійність є незалежними показниками
- усе залежить від інших характеристик вибірки
- рівність нулю різниці середніх значень двох показників
- рівність нулю дисперсій двох показників
- рівність одиниці відношення дисперсій двох показників
- рівність нулю відношення дисперсій двох показників
- рівність нулю різниці середніх значень двох показників
- рівність нулю дисперсій двох показників
- рівність одиниці відношення дисперсій двох показників
- рівність нулю відношення дисперсій двох показників
- ймовірність прийняти неправильну гіпотезу
- ймовірність відхилити правильну гіпотезу
- ймовірність прийняти правильну гіпотезу
- ймовірність відхилити неправильну гіпотезу
- оцінка збігається зі значенням параметра
- математичне сподівання оцінки збігається зі значенням параметра
- математичне сподівання показника відхиляється від оцінки не більше від заданої величини
- математичне очікування пропорційне до дисперсії
- коефіцієнт кореляції Пірсона
- коефіцієнт рангової кореляції Спірмена
- коефіцієнт хі-квадрат
- коефіцієнт дзета-функції Рімана
- функціональної залежності для кількісних показників
- статистичної залежності для якісних показників
- статистичної залежності для кількісних показників
- функціональної залежності для якісних показників
- на скільки одиниць зміниться Y, якщо X збільшиться на 1 одиницю
- на скільки одиниць збільшиться Y, якщо X збільшиться на 1 одиницю
- на скільки одиниць збільшиться X, якщо Y збільшиться на 1 одиницю
- на скільки одиниць зменшиться Y, якщо X збільшиться на 1 одиницю
- кумулята частот
- гістограма частот
- полігон частот
- астролябія частот
- кількість значень показника, які більші за а, але не перевищують b
- відносна частота значень показника, які більші за а, але не перевищують b
- різниця між частотою варіанти b та частотою варіанти а
- емпірична ознака спадковості показника b у відношенні до a
- збільшиться у 2 рази
- збільшиться в 4 рази
- зменшиться у 2 рази
- збільшиться у
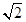 разів
разів
- помножиться на 2
- помножиться на 4
- поділиться на 2
- поділиться на 4
- метод найкоротшого спуску
- метод найменших квадратів
- метод послідовних наближень
- метод спряжених ґрадієнтів
- Стьюдента
- Фішера
- Пірсона хі-квадрат
- Кохрена
- середнє значення квадратів відхилення значень показника від середнього
- сума квадратів відхилення значень показника від середнього
- середнє значення відхилень значень показника від середнього
- сума модулів відхилень значень показника від середнього
- лінійної статистичної залежності для двох кількісних показників
- квадратичної статистичної залежності для двох якісних показників
- статистичної залежності для двох порядкових показників
- статистичної залежності для двох категоріальних (якісних) показників.
- середнього рівня
- розкиду значень
- причини розподілу
- форми розподілу
- виду розподілу
- значення певного параметра заданого розподілу
- співвідношення між значеннями параметрів заданих розподілів
- дисперсії заданих розподілів
- 15
- 14
- 14.5
- 16
- 15
- 14
- 14.5
- 16
- 15
- 14
- 9
- 5
- сильна, із зростанням значень X значення Y в середньому зростають
- слабка, із зростанням значень X значення Y в середньому зростають
- сильна, із зростанням значень X значення Y в середньому спадають.
- слабка, із зростанням значень X значення Y в середньому спадають
- 20% спостережених значень перевищує 30
- 30% спостережених значень перевищує 20
- 70% спостережених значень перевищують 20
- 33% спостережених значень перевищує 20
- 95% спостережених значень містяться в цьому інтервалі
- з імовірністю 0.05 інтервал містить математичне сподівання показника
- з імовірністю 0.95 інтервал містить математичне сподівання показника
- 5% спостережених значень не містяться в цьому інтервалі
- 4.4
- 5
- 5.4
- 5.5
- 4
- 4.5
- 5
- 5.5
- 4
- 4.5
- 5
- 5.5
- 4
- 4.5
- 5
- 5.5
Тема :: Математичний аналіз
- 0
- 0,1
- 1
- 2
- 1/4
- 1/3
- 2/3
- 4/3
- для деякого
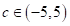 ,
, 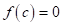
- для деякого
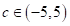 ,
, 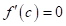
- обидві з перелічених
- немає правильних відповідей
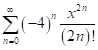 є рядом Тейлора в околі точки
є рядом Тейлора в околі точки - 5,9
- 6,1
- 6,2
- 7
- x = 0
- х = 3
- х = 8
- немає способу сказати
- формула Тейлора
- формула методу хорд
- формула Ейлера
- формула Гауса
- 0.5
- 0.75
- 1
- 0.657
- 576
- 577
- 582
- 575
- 4
- 9
- 3
- 6
- 41
- 40
- 38
- 67
- 1
- -3
- 3
- 5
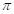
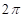
- 7
- 0.5
- 3
- -2
- -4
- -3
- 8
- 1
- 14
- -14
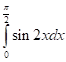 .
.
- 4
- 9
- 1
- 6
- 4
- 96.8
- 3.4
- 103
Тема :: Комп’ютерне моделювання
- опис того чи іншого явища (процесу) за допомогою математичних термінів, формул, рівнянь (алгебраїчних, диференціальних, інтегральних)
- опис фізичного процесу за допомогою математичних термінів
- матричне представлення фізичного явища
- правильної відповіді немає
- дослідження похибок заокруглення
- вивчення алгоритмів обчислення наближених розв’язків задач з неперервної математики
- дослідження кількісних наближень для розв’язків математичних задач, включаючи розгляд похибок
- розділ математики, який займається розробкою та використанням числових методів розв’язування задач
- 6
- 5
- 4
- 3
- 64
- 63
- 15
- 7
- 2 копійки
- 3 копійки
- 4 копійки
- 5 копійок
- абсолютна похибка
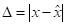 , відносна похибка
, відносна похибка 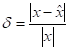
- абсолютна похибка
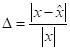 , відносна похибка
, відносна похибка 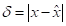
- абсолютна похибка
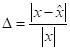 ,
, 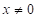 , відносна похибка
, відносна похибка 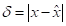
- абсолютна похибка
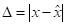 , відносна похибка
, відносна похибка 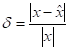 ,
, 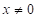
- 315700, точне значення 315690
- 0,0005500, точне значення 0,0005510
, точне значення
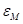 (машинна точність), точне значення 0
(машинна точність), точне значення 0
- Кількість значущих цифр у відповіді дорівнює t.
- Кількість значущих цифр неможливо передбачити через похибки скорочення або заокруглення.
- Кількість значущих цифр приблизно дорівнює lg(Rx).
- Жодне з перерахованих.
- 2
- 3
- 4
- 5
- Відносна похибка завжди менша за абсолютну.
- Відносна похибка може бути меншою за абсолютну за умови, що x достатньо велике.
- Відносна похибка дає краще уявлення про кількість правильних значущих цифр.
- Жодне з перерахованих.
- 100
- 50
- 48
- 25
- 100110,011
- 10011,110
- 11001,011
- 10011,0011
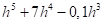
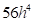
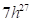
- усі з перерахованих вище
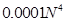
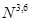
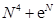
- усі з перерахованих вище
- лінійна
- супер-лінійна
- квадратична
- швидша за квадратичну
- лінійна
- супер-лінійна
- квадратична
- швидша за квадратичну
- 50
- 10
- 100
- 500
- 0,5
- 1
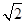
- 2
- процес виконання моделі на комп'ютері
- процес оптимізації коду моделі
- процес перевірки, чи відповідає модель реальним даним
- процес створення моделі
- моделювання клімату не потребує великих обчислювальних потужностей
- модель клімату завжди точна
- враховуються як детерміновані, так і випадкові процеси
- використовуються тільки лінійні рівняння
- комп'ютерна гра, яка імітує реальність
- прототип комп'ютерної програми
- комп'ютерна модель продукту, яка використовується для тестування і аналізу
- фізична модель продукту
- швидкість виконання моделі на комп'ютері
- кількість пам'яті, яку використовує модель
- ступінь, до якого модель реагує на зміни вхідних даних
- здатність моделі точно передавати результати експериментів
- Microsoft Excel
- Notepad
- Blender
- MATLAB
- використовується тільки в країнах ЄС
- використовується лише для лінійних рівнянь
- використовується для статистичного моделювання випадкових процесів
- використовується для вирішення детермінованих задач
- модель, яка заснована на лінійній алгебрі
- модель, яка використовує диференціальні рівняння
- модель, яка імітує поведінку окремих агентів в системі
- модель, яка використовує статистичні методи
- розробка програмного забезпечення для тривимірної графіки
- використання інтернету для створення віртуальних світів
- створення повністю комп'ютеризованого середовища, яке імітує реальний світ
- використання комп'ютерів для створення візуальних ефектів у фільмах
- створення комп'ютерних зображень
- використання комп'ютерів для написання програмного забезпечення
- процес використання комп'ютерів для створення моделей реальних систем
- використання комп'ютерів для створення відеоігор
- метод середніх квадратів
- метод Гауса
- метод Ейлера
- метод Монте-Карло
Тема :: Числові методи лінійної алгебри
- точні та наближені
- непрямі та ітераційні
- точні та збіжні
- аналітичні та експериментальні
- метод Крамера, метод Жордана-Гауса
- простої ітерації
- метод Зейделя
- метод Ньютона
- число, що обчислюється за правилом:
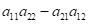
- число, що обчислюється за правилом:
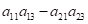
- число, що обчислюється за правилом:
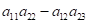
- суму квадратів елементів матриці
- правилом трикутників, правилом Саррюса
- правилом Гауса
- правилом провідників
- правилом правої руки
- Якщо
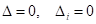 , то існує єдиний розв’язок; система лінійних рівнянь сумісна
, то існує єдиний розв’язок; система лінійних рівнянь сумісна - Якщо
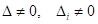 , то існує єдиний розв’язок; система лінійних рівнянь сумісна
, то існує єдиний розв’язок; система лінійних рівнянь сумісна - Якщо
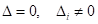 , то існує єдиний розв’язок; система лінійних рівнянь сумісна
, то існує єдиний розв’язок; система лінійних рівнянь сумісна - Якщо вона суміщає сусідні елементи матриці
- Якщо
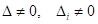 то розв’язків немає; система лінійних рівнянь не сумісна
то розв’язків немає; система лінійних рівнянь не сумісна - Якщо
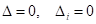 , то розв’язків немає; система лінійних рівнянь не сумісна
, то розв’язків немає; система лінійних рівнянь не сумісна - Якщо
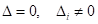 то розв’язків немає; система лінійних рівнянь не сумісна
то розв’язків немає; система лінійних рівнянь не сумісна - Якщо вона не суміщає сусідні елементи матриці
- Якщо
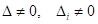 , то є безліч розв’язків; система лінійних рівнянь невизначена
, то є безліч розв’язків; система лінійних рівнянь невизначена - Якщо
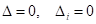 , то є безліч розв’язків; система лінійних рівнянь невизначена
, то є безліч розв’язків; система лінійних рівнянь невизначена - Якщо
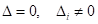 , то є безліч розв’язків; система лінійних рівнянь невизначена
, то є безліч розв’язків; система лінійних рівнянь невизначена - Якщо матриця системи зводиться до верхньої трикутної форми
- полягає у послідовному виключенні змінних з кожних наступних рівнянь і приведенні заданої системи до так званого “трикутного вигляду”
- полягає у виключенні змінних з кожних наступних рівнянь
- полягає у послідовному обчисленні змінних
- полягає у перетворенні системи до вигляду, коли її визначник дорівнює нулю
- матриця, під головною діагоналлю якої всі елементи дорівнюють нулю
- матриця, над головною діагоналлю якої всі елементи дорівнюють нулю
- матриця, всі елементи якої дорівнюють нулю
- матриця, елементи якої відсортовані так, що зростають в напрямах вгору і вправо, утворюючи трикутник
- якщо множини їхніх розв’язків збігаються
- якщо множини їхніх розв’язків не збігаються
- якщо множини їхніх розв’язків не тотожні
- якщо їх праві частини збігаються
- Зміна місцями двох стовпців системи із зміною знаку
- Додавання до одного рядка іншого, помноженого на число нуль
- Множення (ділення) довільного рядка розширеної матриці системи на відмінне від нуля число
- Піднесення елементів рядка системи до певного степеня
- прямий хід і зворотний хід
- прямий і непрямий ходи
- ініціалізація і постобробка
- компілювання та компонування
- з n+1-кроків
- з n+m-кроків
- з n-кроків
- n+2m-кроків
- полягає в тому, що
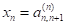 одразу ж прирівняна останній координаті вільних членів
одразу ж прирівняна останній координаті вільних членів - полягає в тому, що система зводиться до такої системи
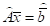
- правильної відповіді немає
- полягає в тому, що в результаті отримаємо систему лінійних рівнянь верхньої трикутної форми, в якій елементи головної діагоналі рівні одиниці, а піддіагональні елементи – нулі.
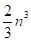 арифметичних операцій
арифметичних операцій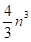 арифметичних операцій
арифметичних операцій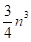 арифметичних операцій
арифметичних операцій- залежить від симетрії системи
- У результаті елементарних перетворень виходить система, еквівалентна вихідній. Або якщо розширену матрицю системи піддати елементарним перетворенням, то одержимо розширену матрицю нової системи, еквівалентну (рівносильну) вихідній.
- Усі елементарні перетворення оборотні (тобто якщо деяка система отримана з вихідної за допомогою елементарних перетворень, то від її можна повернутися до вихідного також за допомогою елементарних перетворень).
- Систему лінійних рівнянь (L) можна перетворити до унарної множини рівнянь (U), що дає можливість безпосередньо звести її до розв’язування сукупності рівнянь першого порядку
- Довільну квадратну дійсну матрицю можна розкласти на добуток двох трикутних матриць, одна з яких є нижньою (лівою) трикутною (L), а друга – верхньою трикутною (U).
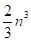 арифметичних операцій
арифметичних операцій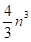 арифметичних операцій
арифметичних операцій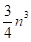 арифметичних операцій
арифметичних операцій- залежить від симетрії системи
- вектором власних значень
- власними векторами
- алгебричним доповненням
- мінором матриці
- комплексними
- чисто уявними
- дійсними
- залежить від конкретних значень коефіцієнтів матриці
- додатними
- від’ємними
- дійсними
- чисто уявними
- 0
- 1
- 100
- 10000
- 1+і, 1-і
- 1+і, 1+і
- 1, 1
- 1-і, 1-і
- метод Ґівенса
- метод Бріджмена – Стокбагера
- метод Якобі
- метод Айнштайна
- верхня трикутна матриця, у якій усі елементи, крім діагональних дорівнюють нулю
- квадратна матриця, у якій усі елементи нижче від першої піддіагоналі дорівнюють нулю
- квадратна матриця, у якій елементи над головною діагоналлю почергово змінюють знак
- верхня трикутна матриця, діагональні елементи якої дорівнюють нулю
- перетворенням Хаусхолдера
- перетворенням Рівіца
- перетворенням Моцарта
- перетворенням Вівальді
Тема :: Методи розв’язування нелінійних рівнянь
- n+2
- n+1
- n
- n-1
- 0
- 1
- 2
- нескінченно багато
- 0
- 1
- нескінченно багато
- залежить від параметра b
- 3
- 2
- 1
- жодного
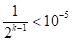
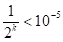
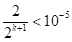
- жодне з переліченого
- на цьому інтервалі повинен бути один корінь рівняння
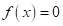
- на цьому інтервалі повинен бути щонайменше один корінь рівняння
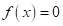
- на цьому інтервалі немає жодного кореня рівняння
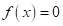
- жодне із переліченого
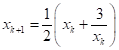 є збіжним, до якого значення він збігається
є збіжним, до якого значення він збігається
- 0,5
- 1,0
- 1,5
- 2,0
- метод Ньютона може мати лінійну збіжність
- метод Ньютона може мати квадратичну збіжність
- метод Ньютона може взагалі не збігатися
- усі тези є вірними
- менша кількість обчислень на одну ітерацію
- швидша збіжність
- краща збіжність далеко від розв’язку
- жодної переваги
- хорошим вибором, оскільки ця точка є екстремумом функції і метод Ньютона збігатиметься швидше
- поганим вибором, оскільки метод Ньютона у цьому випадку не спрацює
- байдуже, адже збіжність залежить від вигляду самої функції, а не її похідної
- байдуже, адже збіжність залежить від кількості кратних коренів
- його можна використати для швидкого і високоточного відшукання наближень для радикалів (коренів певного степеня) чисел
- він є надійним при обчисленні коренів поліномів високих порядків
- він збігається швидше від інших методів числового розв’язування нелінійних рівнянь
- його можна успішно використовувати для обчислення кратних коренів
- логарифмічні, ірраціональні, тригонометричні
- логарифмічні, ірраціональні, степеневі
- ірраціональні, степеневі, тригонометричні
- алгебричні рівняння порядку, вищого за 4
- логарифмічні
- ірраціональні
- тригонометричні
- степеневі рівняння
- точні методи
- збіжні методи
- наближені методи
- системні методи
- функція
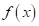 неперервна на
неперервна на 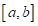
- монотонна функція
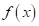 неперервна на
неперервна на 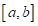 та приймає на початку і в кінці проміжку різні знаки
та приймає на початку і в кінці проміжку різні знаки 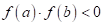
- функція
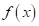 неперервна на
неперервна на 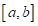 та є монотонно зростаючою
та є монотонно зростаючою - монотонна функція
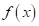 неперервна на
неперервна на 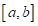 та має додатну першу похідну
та має додатну першу похідну
- потребує знання аналітичного вигляду функції
- метод завжди конвергує до точного розв'язку
- метод є ітераційним і базується на перетворенні рівняння до виду x=g(x)
- використовує другі похідні для наближення кореня
- початкові наближення повинні бути з різними знаками функції
- функція повинна мати похідну
- функція повинна бути монотонною
- початкові наближення повинні бути однаковими
- завжди потребує більше ітерацій, ніж метод хорд
- є швидшим за метод Ньютона-Рафсона
- потребує двох початкових наближень, між якими функція змінює знак
- використовує похідні для пошуку кореня
- метод Гауса
- метод Крамера
- метод хорд
- метод розділення змінних
- метод для розв'язування систем лінійних рівнянь
- метод для інтегрування диференціальних рівнянь
- ітераційний метод для наближення коренів нелінійних рівнянь
- метод для знаходження точного розв'язку лінійних рівнянь
Тема :: Інтерполювання
- так
- ні
- не все так однозначно
- вірної відповіді немає
- інтерполяційний поліном є єдиним
- є безмежна кількість таких поліномів
- відсутні такі інтерполяційні поліноми
- утворений інтерполяційний поліном має аналітичне продовження на кругову область
- інтерполяція
- екстраполяція
- регресія
- апроксимація кривої
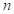
- не більший за
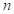
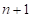
- не менший за
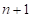
- 1
- 2
- 1 або 2
- безліч
- екстраполяція
- інтерполяція
- регресія
- апроксимація кривої
- 1/6
- 1/9
- 1/64
- 0
- кусково-кубічна інтерполяція дає можливість забезпечити неперервність похідних
- кусково-кубічна інтерполяція загалом швидше збігається до заданої функції швидше, ніж кусково-лінійна
- кусково-кубічна інтерполяція є вигіднішою в обчислювальному сенсі
- кусково-кубічна інтерполяція дає можливість передбачити похідні краще, ніж лінійна
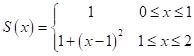 НЕ Є кубічним сплайном. Чому
НЕ Є кубічним сплайном. Чому
- перші похідні
- другі похідні
- перші і другі похідні
- треті похідні
- сплайном
- дедлайном
- хедлайном
- майном
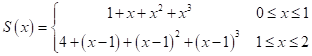 сплайном
сплайном
- так, може
- ні, не може
- залежить від крайових умов
- залежить від дисперсії
- екстраполяцією
- інтерполяцією
- мультипольним розвиненням
- детермінацією
- інтерполяцією методом найближчого сусіда (ступінчастою інтерполяцією)
- інтерполяцією лінійним сплайном
- інтерполяцією квадратичним поліномом
- інтерполяцією кубічним сплайном
- інтерполяція двома лінійними функціями однієї змінної
- узагальнення лінійної інтерполяції для функції двох змінних
- створення білінійної форми функції
- такого терміну не існує
- сплайн-інтерполяція
- кусково-лінійна інтерполяція
- поліном Ньютона
- метод Лагранжа
- проблема, пов'язана з використанням лінійної інтерполяції
- проблема, пов'язана з кусочно-поліноміальною інтерполяцією
- проблема, пов'язана з недостатньою кількістю точок для інтерполювання
- проблема, пов'язана з використанням поліномів високого ступеня на великому інтервалі
- інтерполююча функція, яка використовує експоненціальні функції
- інтерполююча функція, яка використовує квадратичні поліноми
- інтерполююча функція, яка використовує кубічні поліноми для кожного інтервалу
- інтерполююча функція, яка використовує кусково-лінійні функції
- інтерполяція за допомогою експоненціальних функцій
- інтерполяція за допомогою тригонометричних функцій
- інтерполяція за допомогою кусково-лінійних функцій
- інтерполяція за допомогою поліномів високого ступеня
- метод для розв'язання лінійних рівнянь
- кусково-лінійна інтерполяція
- інтерполюючий поліном, що використовує вагові коефіцієнти
- інтерполюючий поліном, що використовує розділені різниці
- метод Ньютона з розділеними різницями
- лінійна інтерполяція
- сплайн-інтерполяція
- метод Лагранжа
- метод побудови раціональних функцій
- метод, що використовує кусково-поліноміальні функції низького ступеня
- метод використання кусково-лінійних функцій
- метод побудови інтерполюючого поліному високого ступеня
- використання великих обчислювальних ресурсів
- гладкість та неперервність першої і другої похідних
- висока точність в точках поза діапазоном даних
- простота розрахунків
- синусоїдальна функція
- поліном Ньютона
- поліном Лагранжа
- експоненціальна функція
- процес апроксимації функції поза межами відомого діапазону даних
- метод для розв'язання диференціальних рівнянь
- процес побудови нових точок в межах відомого діапазону даних
- метод для знаходження максимуму функції
Тема :: Числове інтегрування
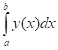
- у заміні на заданому проміжку підінтегральної функції трансцендентною функцією
- у заміні підінтегральної функції інтерполюючою або апроксимуючою функцією простого вигляду (наприклад поліномом) з аналітичним інтегруванням
- в обчисленні підінтегральної функції на проміжку
- у заміні підінтегральної функції логарифмічною
- формули Ньютона-Котеса
- формула методу хорд
- формула методу дотичних
- формули Ілона Маска
- 1/6, 2/3, 1/8
- 1/6, 2/4, 1/8
- 1/6, 2/3, 1/6
- 1/3, 2/3, 1/3
- якщо права частина неперервна в деякій обмеженій області або в деякій півсмузі, де обмеження ставляться лише на деяку півсмугу, і ця функція не задовольняє умову Ліпшіца, то задача має розв’язок і цей розв’язок єдиний
- якщо права частина неперервна в деякій обмеженій області або в деякій півсмузі, де обмеження ставляться лише на деяку півсмугу, і вона задовольняє умову Ліпшіца, то задача має розв’язок і цей розв’язок єдиний
- якщо права частина неперервна в деякій обмеженій області або в деякій півсмузі, де обмеження ставляться лише на деяку півсмугу, то задача має розв’язок і цей розв’язок єдиний
- якщо права частина неперервна в деякій обмеженій області
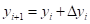 , де
, де 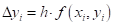
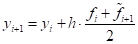
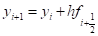
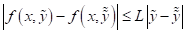
- мала точність (дає практично задовільний результат при малих значеннях кроку)
- даний метод є лінійним алгебраїчним методом
- точний результат
- метод ніколи не є збіжним
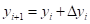 , де
, де 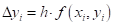
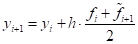
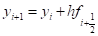
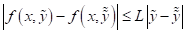
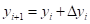 , де
, де 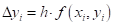
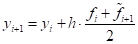
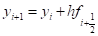
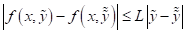
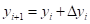 , де
, де 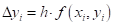
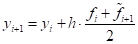
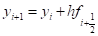
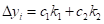
- необхідно, щоб розклад функції “у” в ряд Тейлора в околі точки
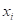 до другого доданка включно узгоджувався з формулою
до другого доданка включно узгоджувався з формулою 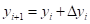
- необхідно, щоб розклад функції “у” в ряд Тейлора в околі точки
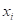 до другого доданка включно узгоджувався з формулою
до другого доданка включно узгоджувався з формулою 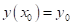
- необхідно, щоб розклад функції “у” в ряд Тейлора в околі точки
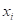 до другого доданка включно узгоджувався з формулою
до другого доданка включно узгоджувався з формулою 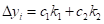
- необхідно, щоб він був удвічі точнішим за метод Ейлера
- всі вони мають досконалу точність
- всі вони є неявними
- всі вони є збіжними
- вони не є збіжним
- воно точне для квадратичних функцій
- під час отримання квадратурних формул нормують квадратичну форму
- у часи Стародавньої Греції обчислення площ складних фігур зводили до визначення площі еквівалентного квадрата
- при побудові відповідних формул використовують розв’язок квадратного рівняння
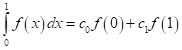 є точною для усіх сталих та лінійних функцій. Визначте значення коефіцієнтів
є точною для усіх сталих та лінійних функцій. Визначте значення коефіцієнтів
- використовує параболи для наближення площі під кривою
- використовує випадкові точки для оцінки інтегралів
- використовує крайні значення функції на інтервалі
- використовує середнє значення функції на інтервалі
- метод, який використовує випадкові точки для оцінки інтегралів
- метод, який використовує трапеції для наближення площі під кривою
- метод, який розбиває інтервал на кілька менших інтервалів і застосовує метод Симпсона до кожного з них
- метод, який використовує один інтервал для оцінки інтегралів
- використовує параболи для наближення площі під кривою
- використовує детерміновані точки для оцінки інтегралів
- використовує змінний крок інтегрування в залежності від функції
- використовує постійний крок інтегрування
- метод, який використовує випадкові точки для оцінки інтегралів
- метод, який використовує параболи для наближення площі під кривою
- метод, який розбиває інтервал на кілька менших інтервалів і застосовує метод трапецій до кожного з них
- метод, який використовує один інтервал для оцінки інтегралів
- метод Монте-Карло
- метод Симпсона
- метод трапецій
- метод прямокутників
- використовує параболи для наближення площі під кривою
- використовує трапеції для наближення площі під кривою
- використовує оптимальні точки та вагові коефіцієнти для оцінки інтегралів
- використовує прямокутники для наближення площі під кривою
- інтегрування, яке використовує параболи
- інтегрування, яке використовує випадкові точки
- інтегрування, яке використовує крайні значення функції на інтервалі
- інтегрування, яке використовує середнє значення функції на інтервалі
- використовує параболи для наближення площі під кривою
- використовує випадкові числа для оцінки інтегралів
- використовує постійний крок інтегрування
- використовує детерміновані точки для оцінки інтегралів
- максимальне значення функції на інтервалі
- величина, яка визначає швидкість виконання методу
- сума значень функції на інтервалі
- різниця між наближеним значенням інтеграла та його точним значенням
- метод, який використовує параболи для наближення площі під кривою
- метод, який використовує оптимальні вагові коефіцієнти та точки для оцінки інтеграла
- метод, який використовує трапеції для наближення площі під кривою
- метод, який використовує прямокутники для наближення площі під кривою
- використовує трикутники для наближення площі під кривою
- використовує параболи для наближення площі під кривою
- використовує трапеції для наближення площі під кривою
- використовує прямокутники для наближення площі під кривою
- метод, який використовує параболи для наближення площі під кривою
- метод, який використовує трапеції для наближення площі під кривою
- метод, який використовує прямокутники для наближення площі під кривою
- метод, який використовує випадкові числа для оцінки інтегралів
- метод, який використовує лінійну апроксимацію функції
- метод, який використовує випадкові числа для оцінки інтегралів
- метод, який змінює крок інтегрування в залежності від функції
- метод, який використовує постійний крок інтегрування
- використовує параболи для наближення площі під кривою
- використовує лінійну апроксимацію функції на інтервалі
- використовує середнє значення функції на інтервалі
- завжди точний метод
- метод Симпсона
- метод Гауса
- метод трапецій
- метод прямокутників
- використовує параболи для наближення площі під кривою
- має велику похибку, особливо на нерівномірних функціях
- використовує середнє значення функції на інтервалі
- завжди точний метод
- метод, який використовує трикутники для наближення площі під кривою
- метод, який використовує параболи для наближення площі під кривою
- метод, який використовує трапеції для наближення площі під кривою
- метод, який використовує прямокутники для наближення площі під кривою
- процес наближення значення інтеграла
- процес розв'язання диференціального рівняння
- процес знаходження точного значення інтеграла
- процес знаходження похідної функції
- метод трапецій
- метод Гауса
- метод прямокутників
- метод Симпсона
- сума площ під параболами
- середнє значення висоти функції, помножене на довжину інтервалу
- середнє арифметичне значення функції на інтервалі
- сума площ під прямокутниками
Тема :: Прикладне програмування. Алгоритми та структури даних
- динамічних структур даних
- напівстатичних структур даних
- інтегрованих структур даних
- простих (базових, примітивних) структур даних
- кількості операцій присвоювання, що виконуються в алгоритмі
- від швидкодії апаратного забезпечення
- від розміру вхідних даних
- від кількості кроків алгоритму
кільцевого списку?
- 2
- 1
- стільки, скільки є елементів у списку
- довільна кількість
- проводиться послідовний перегляд кожного елементу
- проводиться послідовний перегляд кожного елементу від середини таблиці
- проводиться послідовний перегляд кожного елементу від початку масиву до кінця через 1 елемент
- проводиться послідовний перегляд кожного елементу від початку масиву до кінця через 2 елементи
- послідовний перегляд елементів у відсортованому масиві до того часу, поки елемент не буде знайдено
- пошук елементу шляхом послідовного перегляду елементів
- пошук елементу у відсортованому масиві шляхом поділу його навпіл до того часу, поки елемент не буде знайдено
- пошук елементу у масиві шляхом поділу його навпіл до того часу, поки елемент не буде знайдено
- у порядку зростання
- у порядку спадання
- хаотично
- порядок розміщення елементів для бінарного пошуку значення не має
- черга
- стек
- дек
- масив
До стеку застосовано процедуру pop(). Яким біде вміст стеку після цього?
- 3, -4, 12, 0
- -4, 12, 0, 1
- 3, -4, 12, 0, 1, 0
- 0, 3, -4, 12, 0, 1
До черги застосовано процедуру push(2). Яким біде вміст черги після цього?
- 15, 7, -1, 6, 2
- 2, 15, 7, -1, 6
- 15, 2, 7, -1, 6
- 15, 7, -1, 6
Який із алгоритмів пошуку знайде число 285 за меншу кількість порівнянь?
- алгоритм лінійного пошуку
- алгоритм бінарного пошуку
- алгоритм лінійного пошуку з бар'єром
- обидва алгоритми виконають однакову кількість порівнянь
- множина
- дерево
- граф
- послідовність
- він включає допоміжний алгоритм
- він складений так, що його виконання передбачає багатократне повторення одних і тих же дій
- його команди виконуються в порядку їх природного дотримання один за одним незалежно від яких-небудь умов
- хід його виконання залежить від істинності тих або інших умов
- обсяг додаткової пам'яті
- середній час сортування
- тип елементів
- довжина масиву
- формує наступне у прогресії значення
- обчислювальний процес, що викликає сам себе
- елементи множини задаються за допомогою інших елементів цієї ж множини
- використовується для проведення розрахунків над матрицями
int intFunc(int n)
{
if (n==1)
return 1;
else
return intFunc(n-1)+2*n-1;
}
Яке із тверджень про дану функцію правильне?
- ця функція рекурсивна
- функція має один параметр
- це функція, що приймає на вхід аргумент цілого значення, а повертає дійсне
- для значення аргументу 2 функція повертає значення 4
- множина даних та зв’язків між ними
- множина елементів певного типу
- множина елементів, пов’язаних між собою
- набір елементів, тип яких задається
- загальної задачі
- індивідуальної задачі
- моделі задачі
- деякої задачі
- множиною допустимих значень певної структури
- набором допустимих операцій
- описом правил переходу від одного елемента до іншого
- кількістю пам'яті, що виділена для зберігання структури даних
- структура даних із прямим доступом
- фізична структура даних
- лінійна структура даних
- логічна структура даних
- сукупність елементів одного типу, що об’єднані спільним іменем
- сукупність елементів
- сукупність елементів, звернення до кожного із яких відбувається за власним іменем
- іменована область пам’яті, в якій розміщені деякі елементи
- правила виконання певних дій
- опис послідовності дій, чітке виконання яких приводить до рішення поставленої задачі за кінцеве число кроків
- орієнтований граф, який вказує порядок виконання деякого набору команд
- протокол обчислювальної мережі
- набір команд для комп`ютера
- він включає допоміжний алгоритм
- він може бути представлений в табличній формі
- він складений так, що його виконання передбачає багатократне повторення одних і тих же дій
- його команди виконуються в порядку їх природного дотримання один за одним незалежно від яких-небудь умов
- хід його виконання залежить від істинності тих або інших умов
- хід його виконання залежить від істинності тих або інших умов
- він включає допоміжний алгоритм
- він може бути представлений в табличній формі
- його команди виконуються в порядку їх природного дотримання один за одним незалежно від яких-небудь умов
- він складений так, що його виконання передбачає багатократне повторення одних і тих же дій
- його команди виконуються в порядку їх природного дотримання один за одним незалежно від яких-небудь умов
- хід його виконання залежить від істинності тих або інших умов
- він включає допоміжний алгоритм
- він може бути представлений в табличній формі
- він складений так, що його виконання передбачає багатократне повторення одних і тих же дій
- скінченність
- можливість зміни послідовності виконання команд
- циклічність
- можливість виконання алгоритму в зворотному порядку
- результативність
- масовість
- скінченність
- результативність
- детермінованість
- дискретність
- масовість
- детермінованість
- результативність
- дискретність
- скінченність
- скінченність
- детермінованість
- масовість
- дискретність
- результативність
- результативність
- скінченність
- дискретність
- детермінованість
- масовість
- результативність
- детермінованість
- масовість
- скінченність
- дискретність
- програмою
- лістингом
- виконавцем алгоритму
- текстівкою
- протоколом алгоритму
- інструкцію по використанню мобільного телефона
- список студентів групи
- кулінарний рецепт
- перелік обов’язків працівника
- програмою
- блок-схемою
- лістингом
- графічним алгоритмом
- на якому рівні знаходиться поточна позиція пошуку
- чи не є поточний листовий вузол шуканим
- в якому відношенні (більше / менше) ключ поточного вузла знаходиться з шуканим ключем
- в якому відношенні (більше / менше) ключ поточного вузла знаходиться з його правим або лівим нащадком
- стек
- черга
- деки
- Так
- Ні
- клавіш, натиснутих користувачем в процесі написання листа
- повідомлень про неминучі зовнішні загрози для зорельота «Ентерпрайз»
- елементів, автоматично сортованих при вставці
- символічних імен оброблюваного алгебраїчного виразу
- Свобода вибору адреси
- Пошук іншої комірки в масиві в тому випадку, якщо вихідна комірка зайнята
- Наявність в масиві багатьох вільних комірок
- Перевірка комірок x + 1, x + 2 і т. д., поки не буде знайдена порожня комірка
- 3
- 1
- 2
- LIFO
- FIFO
- Людина знає, як сортувати, а комп'ютеру необхідно все пояснювати
- Комп'ютер за один раз може порівнювати тільки два об'єкти
- Люди краще справляються з винаходом нових алгоритмів
- Комп'ютер може працювати з даними фіксованого розміру
- кількість літер у назві масиву
- кількість елементів
- кількість індексів
- іноді збільшує час вставки
- завжди збільшує час вставки
- збільшує час виконання всіх операцій;
- збільшує час пошуку в деяких ситуаціях
- Ні
- Так
- Операція вилучення зі стека значно простіша, ніж операція вилучення з черги.
- Вершина стека є повним аналогом початку черги.
- У черзі можливий циклічний переніс, а в стеку - ні.
- Як в стеку, так і в черзі послідовно видалені елементи розташовуються в комірках з наростаючими значеннями індексів масиву.
- він відображає відношення сусідства між елементами
- всі його елементи розміщено в одну лінію
- алгоритм його сортування має лінійну складність
- копіювання і порівняння
- переміщення і порівняння
- переміщення і копіювання
- порівняння і перестановки
- відсортовані елементи накопичуються справа
- елементи з найбільшими значеннями ключа накопичуються зліва (малі значення індексів)
- багаторазово знаходиться значення мінімального ключа
- для правильної вставки кожного елемента доводиться зсувати кілька елементів
- стек
- черга
- деки
- Кількість вхідних даних
- Кількість елементарних кроків алгоритму
- Кількість секунд (годин) роботи
- 10
- 40
- 20
- 30
- полів шахової дошки в ігровій програмі
- натискань клавіш на клавіатурі
- пасажирів, яких таксі повинно підібрати в різних частинах міста
- планет в моделі Сонячної системи
- вказівник
- ім'я масиву
- індекс
- Ні
- Так
- швидше виконується вставка
- швидше виконується створення
- набагато швидше виконується видалення
- швидше виконується пошук
- Ні
- Так
- він взагалі не переміщається
- від молодших індексів до старших
- від старших індексів до молодших
- 35
- 15
- 25
- 45
- кількість індексів елемента масиву
- кількість елементів у масиві
- цілої та дробової частин
- значення елемента даних і вказівника на наступний елемент списку
- дійсної та уявної частин
- функцію зв'язку
- кількість елементів списку
- посилання на перший елемент списку
- вказівник на пусте місце
- вказівник на перший елемент
- поле є порожнім
- ключ кожного лівого нащадка менше, ніж у батька, а ключ кожного правого нащадка більше ключа батька (або дорівнює йому)
- на шляху від кореня до кожного листового вузла ключ кожного вузла більше (або дорівнює) ключа його батька
- у кожного нелистового вузла є нащадки, ключі яких менше (або рівні) ключа батька
- вузол може мати не більше двох нащадків
- що має форму парасольки
- в якому кількість лівих нащадків у кореневого або іншого вузла значно перевищує кількість правих нащадків (або навпаки)
- в якому значення більшості ключів більше середнього арифметичного
- що володіє непередбачуваною поведінкою
- середній час сортування
- довжина масиву
- обсяг додаткової пам’яті
- тип елементів масиву
Позначте всі правильні відповіді.
- z = mas[j]
- mas[i] = mas[j]
- mas[j] = z
- mas[i] = z
- z=mas[i]
- прямому переборі елементів масиву
- випадковому виборі елементів масиву
- упорядкуванні масиву
- поділенні масиву на дві рівні частини
- пошук тільки у списку
- пошук виходу з лабіринту
- пошук у масиві
- пошук чергового ходу гри в шахи
- в обох
- ліворуч
- праворуч
- ланцюжок
- виконавець
- комп’ютер
- команда
- слідування
- розгалуження
- циклу
- вибору
- Функція, яка в процесі роботи може викликати саму себе.
- Функція, яка в процесі роботи може довільну кількість разів викликати іншу функцію.
- Функція, яка в процесі роботи може змінювати глобальні змінні.
- Функція, яка в процесі роботи не змінює вхідні параметри.
- на перший елемент
- на 0
- на порожній елемент
- ні на що
- швидке сортування
- сортування бульбашкою
- шейкер-сортування
- це самостійний метод сортування
- кількість викликів рекурсії починаючи із виклику функцією самої себе
- кількість пам’яті, необхідної при виклику рекурсивної функції
- розмір змінної, яка задається при виклику рекурсії
- довжина максимального шляху від початкового виклику до одного із елементарних значень функції
- функція залежності витраченого часу від розміру вхідних даних
- кількість змінних, яка використовується при роботі алгоритму
- функція залежності витраченої пам’яті від розміру вхідних даних
- функція залежності об’єму роботи, яка виконується деяким алгоритмом, від об’єму вхідних даних
- передачою за посиланням
- циклом
- кількома функціями
- глобальною змінною