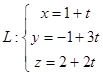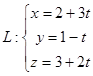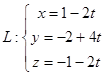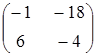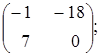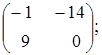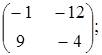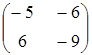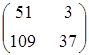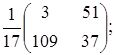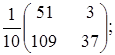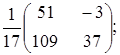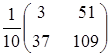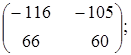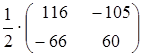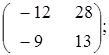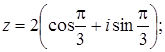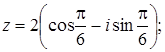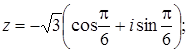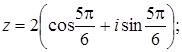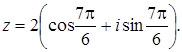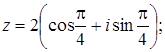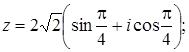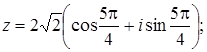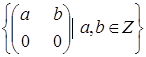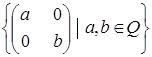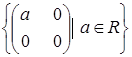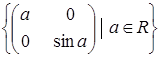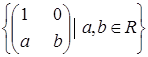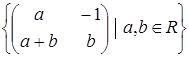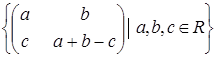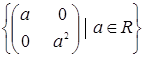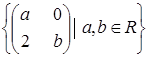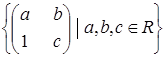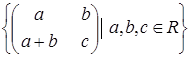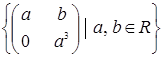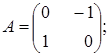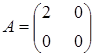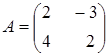Тема :: Аналітична геометрія
При
яких значеннях
х
та
у
вектори
![]() і
і
![]() є колінеарними?
є колінеарними?
-
(2,8)
-
(4,-5)
-
(-8,10)
-
(7,3)
-
(4,0)
Дано
точки
![]() і
і
![]() . Знайти відстань
від початку координат
. Знайти відстань
від початку координат
![]() до
середини відрізка
до
середини відрізка
![]()
-
18
-
13
-
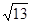
-
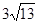
-
3
Дано
вектори
![]() . Знайти
. Знайти
![]() .
.
-
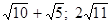
-
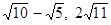
-
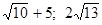
-
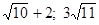
-
2; 9
Обчислити
довжину вектора
![]() , якщо
, якщо
![]() .
.
-
9
-
3
-
5
-
15
-
7
Обчислити
довжину вектора
![]() .
.
-
3
-
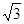
-
7
-
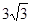
-
4
Знайдіть
кут між векторами
![]() .
.
Обчислити
скалярний добуток векторів
![]() ,
якщо
,
якщо
![]()
-
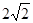
-
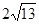
-
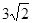
-
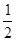
-
2
Знайти
косинус кута α між прямими
![]() і
і
![]() .
.
-
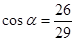
-
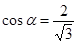 ;
;
-
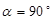
-
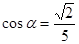
-
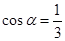
Написати
рівняння прямої, яка проходить через точку А(4,3,0) і паралельна вектору
![]() (–1,1,1).
(–1,1,1).
Знайти
рівняння площини, яка проходить через точки
![]() (1,2,–1)
,
(1,2,–1)
,
![]() (–1,0,4)
,
(–1,0,4)
,
![]() (–2,–1,1).
(–2,–1,1).
-
2 x – y – 3z+2=0
-
x – y+1=0
-
y – z – 1=0
-
x+z – 1=0
-
x – y+z+2= 0
Знайти відстань між паралельними площинами
5 x +3 y –4 z +15=0
15 x +9 y – 12 z – 5=0
-
d=2
-
d=4
-
d=5
-
d=
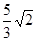
-
d=1
Загальне
рівняння площини, що відповідає рівнянню
![]()
-
3 x-2y+5z+2=0
-
2x-5y+z+1=0
-
x+y+2z-1=0
-
x-2y-z+2=0
-
x+3y-2z+6= 0
Перевірити
чи лежить пряма
![]() на
площині 4
x
+3
y
-
z
+3=0.
на
площині 4
x
+3
y
-
z
+3=0.
-
Лежить
-
Не лежить
-
Такої прямої не існує
-
Такої площини не існує
Написати рівняння еліпса, якщо півосі його відповідно рівні 4 і 2.
Написати рівняння гіперболи, осі якої співпадають з осями координат, якщо відстань між вершинами дорівнює 8, а відстань між фокусами 10.
Скласти
рівняння кола, центр якого міститься в точці А(-3;5) і
![]()
Яка
поверхня задана рівнянням
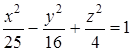
-
однопорожниний гіперболоїд
-
двопорожниний гіперболоїд
-
параболоїд обертання
-
еліпсоїд
Вияснити тип кривої
![]()
-
еліптична
-
параболічна
-
гіперболічна
В паралелограмі
![]() дано вершини
А(1,0,1), В(1,2,9), С(5,6,11). Визначити четверту вершину
D
.
дано вершини
А(1,0,1), В(1,2,9), С(5,6,11). Визначити четверту вершину
D
.
-
(5,2,3)
-
(8,3,1)
-
(-5,3,7)
-
(5,4,3)
-
(-1,0,2)
Знайдіть таке число
k
, щоб виконувалась рівність
![]() ,
коли відомо, що вектори
,
коли відомо, що вектори
![]() протилежно
напрямлені і
протилежно
напрямлені і
![]() .
.
-
-4
-
20
-
-1
-
5
-
7
Знайти координати вектора
![]() , що є колінеарним
до вектора
, що є колінеарним
до вектора
![]() і задовольняє умову
і задовольняє умову
![]() .
.
-
(6,15,5)
-
(-9,12,-3)
-
(-9,3,-12)
-
(3,15,9)
-
(4,0,2)
Обчислити скалярний добуток векторів
![]() , якщо
, якщо
![]()
-
5
-
9
-
-4
-
3
-
6
Обчислити площу паралелограма, побудованого на векторах
![]() , що виходять з
однієї точки.
, що виходять з
однієї точки.
-
13
-
24
-
15
-
3
-
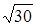
Обчислити скалярний добуток векторів
![]() , якщо
, якщо
![]()
-
5
-
-4
-
-3
-
3
-
6
Через точку М(1,-1,2) провести пряму, паралельну
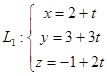 .
.
Рівняння площини, що проходить через точку
![]() (2,3,-1) паралельно
до площини
(2,3,-1) паралельно
до площини
![]() :2
x
-3
y
+5
z
-4=0.має
вигляд:
:2
x
-3
y
+5
z
-4=0.має
вигляд:
-
x+y+z+10=0
-
x+2y+3z-1=0
-
2x+3y-z+10=0
-
3x-2y-5z-12=0
-
2 x-3y+5z+10=0
Знайти точку перетину прямої
![]() з площиною
x
+
y
-2
z
-4=0.
з площиною
x
+
y
-2
z
-4=0.
-
A(2,3,0)
-
A(-2,0,-3)
-
A(0,0,0)
-
A(0,1,3)
Написати рівняння площини, яка проходить
через точку (3,1,-2) і через пряму
![]() .
.
-
x+y+z+10=0
-
x+2y+3z-1=0
-
8 x -9 y- 22 z -59 =0
-
3x-2y-5z-12=0
Написати рівняння параболи, директриса якої
має рівняння
![]() .
.
Знайти
центр кривої
![]()
-
(-1;2)
-
(0;1)
-
(-1;-1)
-
(3;-4)
Знайти
довжину вектора
![]() , якщо
, якщо
![]() ,
,
![]() :
:
-
2
-
3
-
1
-
-2
-
5
Дано
точки
![]() ,
,
![]() . Знайти
х
та
у
відповідно, якщо
. Знайти
х
та
у
відповідно, якщо
![]()
-
(3,1)
-
(-1,-3)
-
(1,3)
-
(2,0)
-
(1;4)
Дано
точки
![]() і
і
![]() .Знайти відстань від
початку координат
.Знайти відстань від
початку координат
![]() до
середини відрізка
до
середини відрізка
![]() .
.
-
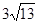
-
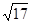
-
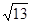
-
13
-
2
При
якому значенні
![]() вектори
вектори
![]() і
і
![]() колінеарні?
колінеарні?
-
0,3
-
0,5
-
1,5
-
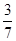
-
4
Знайти
суму векторів
![]() і
і
![]() .
.
-
(1,0)
-
(-5,7)
-
(1,9)
-
(-3,2)
-
(2,0)
Дано
вектори
![]() і
і
![]() . Знайдіть довжину
вектора
. Знайдіть довжину
вектора
![]() .
.
-
11
-
6
-
13
-
15
-
7
Відомо,
що вектори
![]() колінеарні.
Знайдіть
m
.
колінеарні.
Знайдіть
m
.
-
-2
-
3
-
2
-
15
-
1
Знайти
координати вектора
![]() , якщо
, якщо
![]() ,
,
![]() .
.
-
(1,8,2)
-
(1,2,-1)
-
(-1,0,2)
-
(-1,2,1)
-
(0,1,3)
Знайти
довжину вектора
![]() , якщо
, якщо
![]() ,
,
![]() .
.
-
2
-
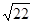
-
1
-
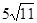
-
6
При
яких значеннях
х
та
у
вектори
![]() і
і
![]() є колінеарними?
є колінеарними?
-
(2,8)
-
(4,-5)
-
(-8,10)
-
(7,3)
-
(4,0)
Дано
точки
![]() і
і
![]() . Знайти відстань
від початку координат
. Знайти відстань
від початку координат
![]() до
середини відрізка
до
середини відрізка
![]()
-
18
-
13
-
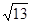
-
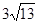
-
3
Тема :: Дискретна математика
Які речення, з наведених нижче, не є висловленнями?
-
Чи існує число менше за 10?
-
Сніг чорний.
-
ln 1= 0
-
2- 4=6
-
2+3
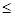 5
5
Які речення, з наведених нижче, є висловленнями?
-
3+5=9
-
4 х = 7
-
Дніпро – велика річка .
-
Трикутник, у якого всі сторони різні, називається рівностороннім.
-
2+5х
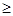 25
25
Які речення, з наведених нижче, є висловленнями?
-
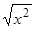 =
x
=
x
-
4 х
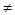 7
7
-
Дніпро – мала річка .
-
7 – просте число.
-
24+х=2
Формули, які на всіх наборах значень своїх атомів набувають значення 1, називають:
-
тавтологіями
-
суперечностями
-
виконуваними
-
нейтральними
-
висловленнями
Формули, які на всіх наборах значень своїх атомів набувають значення 0, називають:
-
тавтологіями
-
суперечностями
-
виконуваними
-
нейтральними
-
тотожно істинними формулами
Формули, для яких значення істинності збігаються в усіх інтерпретаціях цих формул, називають:
-
тавтологіями
-
суперечностями
-
виконуваними
-
нейтральними
-
рівносильними
Оберіть вирази, які відповідають законам ідемпотентності:
Оберіть вирази, які відповідають законам комутативності:
Речення, яке містить змінні і, не будучи висловленням, перетворюється у нього при заміні цих змінних назвами елементів відповідної множини, називають:
-
тавтологією
-
предикатом
-
виконуваним
-
квантором
-
теоремою
Операція кон’юнкції для висловлень А та В є істинною тоді й тільки тоді, коли:
-
А і В є хибними
-
А і В є істинними
-
А є хибним, а В - істинним
-
А є істинним, а В - хибним
-
завжди істинна
Операція диз’юнкції для висловлень А та В є хибною тоді й тільки тоді, коли:
-
А і В є хибними
-
А і В є істинними
-
А є хибним, а В - істинним
-
А є істинним, а В- хибним
-
завжди істинна
Операція імплікації для висловлень А та В є хибною тоді й тільки тоді, коли:
-
А і В є хибними
-
А і В є істинними
-
А є хибним, а В- істинним
-
А є істинним, а В - хибним
-
завжди істинна
Операція еквіваленції для висловлень А та В є істинною тоді й тільки тоді, коли:
-
А і В одночасно істинні або одночасно хибні
-
А і В є істинними
-
А є хибним, а В - істинним
-
А є істинним, а В - хибним;
-
завжди істинна
Які
з наведених формул є рівносильними формулі
![]() ?
?
Які
з наведених формул є рівносильними формулі
![]() ?
?
У
формулі
![]() змінна
змінна
![]() називається:
називається:
-
зв’язаною
-
вільною
-
не вільна й не зв’язана
-
істинною
-
хибною
У
формулі
![]() змінна
змінна
![]() називається:
називається:
-
зв’язаною
-
вільною
-
не вільна й не зв’язана
-
істинною
-
хибною
Множина, яка не містить елементів, називається:
-
скінченною
-
порожньою
-
універсальною
-
булеаном
-
предикатом
Як задається множина переліком елементів?
-
перелічуються усі елементи множини у круглих дужках
-
перелічуються усі елементи у квадратних дужках
-
перелічуються усі елементи у фігурних дужках
-
перелічуються усі елементи у стовпчик
-
перелічуються перші три елементи у фігурних дужках
Які з множин не є підмножинами множини {3, 5, 7, 9}?
-
{3, 5}
-
{{3, 5}, 7, 9}
-
{3, 5, 7, 9}
-
Ø
-
{3}
Оберіть вираз, який відповідає означенню операції об’єднання множини А та множини В:
-
А
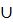 В ={ х:
x
В ={ х:
x
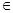 А \/ х
А \/ х
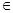 В}
В}
-
А
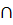 В ={ х:
x
В ={ х:
x
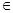 А /\ х
А /\ х
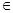 В}
В}
-
А\В = {х: х
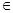 А /\ х
А /\ х
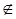 В}
В}
-
А
 В =(А \ В)
В =(А \ В)
 ( В \ А)
( В \ А)
-
А = В
 (А
(А
 В /\ В
В /\ В
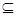 А)
А)
Оберіть вираз, який відповідає означенню операції перерізу множини А та множини В:
-
А
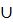 В ={ х:
x
В ={ х:
x
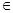 А \/ х
А \/ х
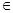 В}
В}
-
А
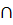 В ={ х:
x
В ={ х:
x
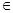 А /\ х
А /\ х
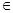 В}
В}
-
А\В = {х: х
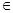 А /\ х
А /\ х
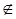 В}
В}
-
А
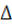 В =(А \ В)
В =(А \ В)
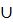 ( В \ А)
( В \ А)
-
А = В
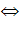 (А
(А
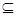 В /\ В
В /\ В
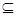 А)
А)
Як називається операція над множинами А та В , якщо її результат складається з тих і тільки тих елементів, які належать множині А і не належать множині В ?
-
об’єднанням множин А та В
-
перерізом множин А та В
-
різницею множин А та В
-
різницею множин В та А
-
симетричною різницею множин А та В
Як називається операція над множинами А та В , якщо її результат складається з тих і тільки тих елементів, які належать одночасно множині А та множині В ?
-
об’єднанням множин А та В
-
перерізом множин А та В
-
різницею множин А та В
-
різницею множин В та А
-
симетричною різницею множин А та В
Як називається операція над множинами А та В , якщо її результат складається з тих і тільки тих елементів, які належать хоча б одній із множин А та В ?
-
об’єднанням множин А та В
-
перерізом множин А та В
-
різницею множин А та В
-
різницею множин В та А
-
симетричною різницею множин А та В
Множина А називається підмножиною множини В , якщо:
-
кожен елемент В є елементом множини А
-
кожен елемент А є елементом множини В
-
кожен елемент В є елементом множини А і, навпаки, кожен елемент А є елементом множини В
-
множина В містить елементи множини А
-
множина А містить елементи множини В
Оберіть множини, які є порожніми:
-
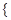 Ø
Ø
-
 х: х –
дільник числа 100
х: х –
дільник числа 100
-
 х: х – буква
слова « математика»
х: х – буква
слова « математика»
-
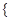 х: х –
розв’язок рівняння
sin
x
=1
х: х –
розв’язок рівняння
sin
x
=1
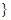
-
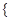 х: х –
розв’язок рівняння
sin
x
=2
х: х –
розв’язок рівняння
sin
x
=2
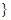
Дві множини А та В називаються рівними, якщо вони складаються з:
-
упорядкованих пар
-
однакової кількості елементів
-
одних і тих самих елементів
-
чисел
-
елементів універсальної множини
Множина, елементами якої є всі підмножини множини А , називається:
-
підмножиною множини А
-
універсальною множиною
-
порожньою множиною
-
власною підмножиною множини А
-
булеаном множини А
Оберіть
із поданих назв законів алгебри множин той, який відповідає виразам
![]() :
:
-
асоціативний закон
-
дистрибутивний закон
-
комутативний закон
-
закон ідемпотентності
-
закон поглинання
Оберіть
із поданих назв законів алгебри множин той, який відповідає виразам
![]() :
:
-
асоціативний закон
-
дистрибутивний закон
-
комутативний закон
-
закон ідемпотентності
-
закон поглинання
Оберіть
із поданих назв законів алгебри множин той, який відповідає виразам
![]() :
:
-
асоціативний закон
-
дистрибутивний закон
-
комутативний закон
-
закон ідемпотентності
-
закон поглинання
Оберіть вирази, які відповідають законам де Моргана:
-
А
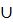 А = А; А
А = А; А
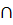 А = А
А = А
-
А
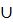 B
= В
B
= В
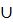 А; А
А; А
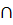 B
=В
B
=В
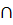 А
А
-
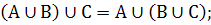
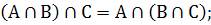
-
(А
 В)
В)
 С = А
С = А
 С
С
 В
В
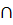 С;
С;
(А
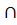 В)
В)
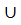 С = (А
С = (А
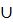 С )
С )
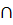 (В
(В
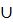 С)
С)
-
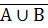 =
=
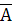
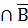 ;
;
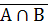 =
=
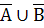
Прямим добутком множин А та В називається:
-
множина спільних елементів А та В
-
множина упорядкованих пар елементів (а;в), де
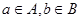
-
множина всіх упорядкованих пар елементів (а;в), де
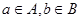
-
множина всіх упорядкованих пар елементів (а;в), де
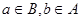
-
множина всіх упорядкованих пар елементів (а;в), де
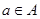
Оберіть вираз, який відповідає означенню операції декартового добутку множин А та В :
Бінарне
відношення
![]() , задане на множині
, задане на множині
![]() , називається на цій
множині рефлексивним, якщо:
, називається на цій
множині рефлексивним, якщо:
Бінарне
відношення
![]() ,
задане на множині
,
задане на множині
![]() ,
називається на цій множині антирефлексивним, якщо:
,
називається на цій множині антирефлексивним, якщо:
Бінарне
відношення
![]() ,
задане на множині
,
задане на множині
![]() ,
називається на цій множині симетричним, якщо:
,
називається на цій множині симетричним, якщо:
Бінарне
відношення
![]() , задане на множині
, задане на множині
![]() , називається на цій
множині антисиметричним, якщо:
, називається на цій
множині антисиметричним, якщо:
Відношення
![]() , задане на множині
А, називається на цій множині відношенням еквівалентності, якщо воно:
, задане на множині
А, називається на цій множині відношенням еквівалентності, якщо воно:
-
симетричне й транзитивне
-
рефлексивне й транзитивне
-
рефлексивне, антисиметричне й транзитивне
-
антирефлексивне, симетричне й транзитивне
-
рефлексивне, симетричне й транзитивне
Зліченною множиною є:
-
множина всіх дійсних чисел з інтервалу (0,1)
-
множина всіх дійсних чисел з сегменту [0,1]
-
об’єднання скінченої кількості скінченних множин
-
будь-яка підмножина зліченної множини
-
множина еквівалентна множині натуральних чисел
Множина, рівнопотужна множині всіх дійсних чисел з інтервалу (0,1), називається:
-
зліченною
-
континуальною
-
скінченною
-
порожньою
-
впорядкованою
Бінарна операція « * » називається на множині А асоціативною, якщо
-
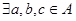 :
(а
*
в)
*
с
= а
*
(в
*
с)
:
(а
*
в)
*
с
= а
*
(в
*
с)
-
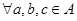 :
(а
*
в)
*
с
= а
*
(в
*
с)
:
(а
*
в)
*
с
= а
*
(в
*
с)
-
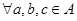 :
(а+в)
*
с=а
*
с+в
*
с
:
(а+в)
*
с=а
*
с+в
*
с
-
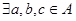 :
(а+в)
*
с=а
*
с+в
*
с
:
(а+в)
*
с=а
*
с+в
*
с
-
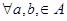 :
а
*
в =
в
*
а
:
а
*
в =
в
*
а
Бінарна операція « * » називається на множині А комутативною, якщо
-
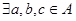 :
(а
*
в)
*
с
= а
*
(в
*
с)
:
(а
*
в)
*
с
= а
*
(в
*
с)
-
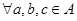 :
(а
*
в)
*
с
= а
*
(в
*
с)
:
(а
*
в)
*
с
= а
*
(в
*
с)
-
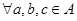 :
(а+в)
*
с=а
*
с+в
*
с
:
(а+в)
*
с=а
*
с+в
*
с
-
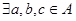 :
(а+в)
*
с=а
*
с+в
*
с
:
(а+в)
*
с=а
*
с+в
*
с
-
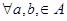 :
а
*
в =
в
*
а
:
а
*
в =
в
*
а
Знайдіть переріз множин А та В, якщо
А={х : 2< х < 5 }, В={х: -2 ≤ х < 3 }.
-
А
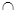 В={х : 2< х <
5 }
В={х : 2< х <
5 }
-
А
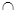 В={х : -2< х
< 3 }
В={х : -2< х
< 3 }
-
А
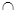 В={х : -2< х
< 5 }
В={х : -2< х
< 5 }
-
А
 В={х : 2< х <
3 }
В={х : 2< х <
3 }
-
А
 В={х : -2< х
< 2 }
В={х : -2< х
< 2 }
Знайдіть
прямий добуток множин А =
![]() та
В =
та
В =
![]() .
.
-
А
 В = {(а,в) : (2 <
а < 5)
В = {(а,в) : (2 <
а < 5)
 (3 < в < 4)
}
(3 < в < 4)
}
-
А
 В = {(2;3), (2;4),
(5;3), (5;4)}
В = {(2;3), (2;4),
(5;3), (5;4)}
-
А
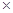 В = {(а,в) : (2
< а < 5)
В = {(а,в) : (2
< а < 5)
 (3
(3
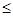 в < 4)}
в < 4)}
-
А
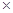 В = {(2;3), (2;4)}
В = {(2;3), (2;4)}
-
А
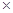 В = {а : (2 < а
< 5)
В = {а : (2 < а
< 5)
 (3
(3
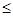 в < 4)}
в < 4)}
Кількість можливих комбінацій з n елементів по k дорівнює:
-
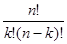
-
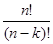
nk-
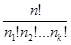
-
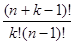
Кількість можливих комбінацій з n елементів по k із повтореннями дорівнює:
-
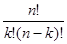
-
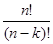
nk-
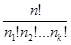
-
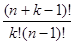
Скінчений зв’язний граф, який не містить циклів, називають
-
лісом
-
платоновим
-
деревом
-
повним
-
двочастинним
Скільки існує способів розміщення на полиці 3 книжок?
-
1
-
6
-
3
-
2
-
18
Тема :: Лінійна алгебра
Яке з тверджень правильне:
-
сума двох розв’язків неоднорідної системи лінійних рівнянь є розв’язком цієї системи
-
сума двох розв’язків неоднорідної системи лінійних рівнянь є розв’язком відповідної однорідної системи рівнянь
-
різниця двох розв’язків неоднорідної системи лінійних рівнянь є розв’язком відповідної однорідної системи рівнянь
-
сума розв’язку неоднорідної системи лінійних рівнянь і розв’язку відповідної системи рівнянь є розв’язком однорідної системи рівнянь
В
якому випадку ранг квадратної матриці
![]() порядку
порядку
![]() дорівнює
дорівнює
![]() :
:
-
якщо
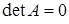
-
якщо
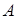 діагональна матриця
діагональна матриця
-
якщо
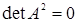
-
якщо
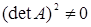
Нехай
![]() – квадратна матриця
порядку
– квадратна матриця
порядку
![]() . Яке з даних
тверджень правильне:
. Яке з даних
тверджень правильне:
-
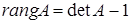
-
якщо
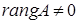 , то
, то
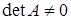
-
якщо
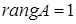 , то
, то
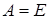
-
якщо
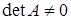 , то
, то
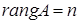
Нехай
![]() – деяка матриця.
Яке з даних тверджень правильне:
– деяка матриця.
Яке з даних тверджень правильне:
-
якщо
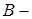 ненульова матриця, а
добуток
ненульова матриця, а
добуток
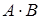 визначений, то
визначений, то
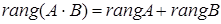
-
стовпцевий ранг матриці
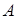 дорівнює
її рядковому рангу
дорівнює
її рядковому рангу
-
сума стовпцевого й рядкового рангів матриці дорівнює
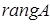
-
сума стовпцевого й рядкового рангів матриці дорівнює нулю
Яке з даних тверджень є правильним:
-
детермінант добутку двох матриць дорівнює сумі їх детермінантів
-
детермінант добутку двох матриць дорівнює добутку їх детермінантів
-
детермінант добутку двох квадратних матриць дорівнює добутку їх детермінантів
-
детермінант добутку двох квадратних матриць дорівнює сумі їх детермінантів
При
якому значенні
![]() ранг
матриці
ранг
матриці
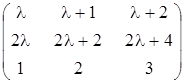 дорівнює 1?
дорівнює 1?
-
5
-
3
-
1
-
-2
-
4
Яка
з вказаних матриць є добутком
![]() матриць
матриць
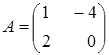 і
і
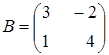 :
:
![]()
Розв’язати
матричне рівняння
![]() ,
якщо
,
якщо
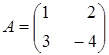 ,
,
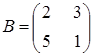 ,
,
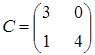 . Вказати правильну
відповідь.
. Вказати правильну
відповідь.
Розв’язати
матричне рівняння
![]() ,
якщо
,
якщо
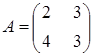 ,
,
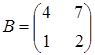 ,
,
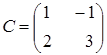 . Вказати правильну
відповідь.
. Вказати правильну
відповідь.
Знайти
детермінант добутку матриць
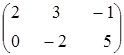 і
і
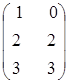 :
:
-
5
-
10
-
13
-
22
-
-45
Знайти
детермінант добутку матриць
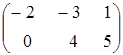 і
і
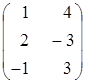 :
:
-
-39
-
-8
-
5
-
0
-
7
Знайти
детермінант добутку матриць
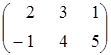 і
і
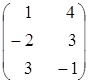 .
.
-
-85
-
65
-
5
-
-99
-
100
Розв’язати
матричне рівняння
![]() , якщо
, якщо
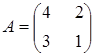 ,
,
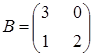 ,
,
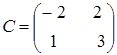 .
.
Знайти суму компонент розв’язку системи лінійних рівнянь
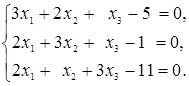
-
4
-
3
-
-3
-
7
-
0
Знайти
суму компонент розв’язку системи лінійних рівнянь
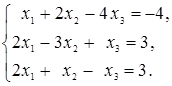
-
7
-
4
-
5
-
-2
-
-9
Знайти
дійсну частину числа
![]() .
.
-
2
-
4
-
-3
-
7
-
3
Знайти
дійсну частину числа
![]() .
.
-
-2
-
2
-
-3
-
5
-
10
Знайти
уявну частину числа
![]()
-
8
-
-5
-
-23
-
9
-
-6
Вказати
тригонометричну форму комплексного числа
![]() :
:
Вказати
тригонометричну форму комплексного числа
![]() :
:
Знайти
остачу від ділення многочлена
![]() на
на
![]() .
.
-
54
-
78
-
-135
-
-133
-
-87
Знайти
остачу від ділення многочлена
![]() на
на
![]() .
.
-
38
-
23
-
-54
-
-27
-
35
Знайти
значення третьої похідної многочлена
![]() від 2, не шукаючи
самої похідної.
від 2, не шукаючи
самої похідної.
-
524
-
336
-
78
-
-478
-
264
Знайти
значення третьої похідної многочлена
![]() при
при
![]() ,
не
шукаючи самої похідної.
,
не
шукаючи самої похідної.
-
162
-
65
-
278
-
32
-
-24
Знайти
кратність кореня
![]() многочлена
многочлена
![]()
-
1
-
2
-
3
-
4
-
0
Яка
з даних множин
![]() вимірних
векторів є векторним підпростором арифметичного простору
вимірних
векторів є векторним підпростором арифметичного простору
![]()
![]() :
:
Знайти
кратність кореня
![]() многочлена
многочлена
![]()
-
1
-
2
-
3
-
4
-
5
Яка з даних множин матриць є підпростором векторного простору квадратних матриць другого порядку з дійсними елементами:
Яка
з даних множин матриць утворює векторний простір над полем
![]() відносно операцій
додавання матриць та множення матриці на число:
відносно операцій
додавання матриць та множення матриці на число:
Яка
з даних множин є лінійно незалежною підмножиною векторного простору
![]() :
:
Нехай
![]() векторний простір
над полем
векторний простір
над полем
![]() .
.
![]() векторний підпростір
простору
векторний підпростір
простору
![]() . Яке із вказаних
тверджень є правильним:
. Яке із вказаних
тверджень є правильним:
Яка
з даних множин матриць утворює векторний простір над полем
![]() відносно операцій
додавання матриць та множення матриці на число:
відносно операцій
додавання матриць та множення матриці на число:
Яка
з даних множин є лінійно незалежною підмножиною векторного простору
![]() :
:
Нехай
![]() векторний простір
над полем
векторний простір
над полем
![]() . Яке із вказаних
тверджень є правильним:
. Яке із вказаних
тверджень є правильним:
Який кут у градусах утворюють вектори
![]() ?
?
-
30
-
45
-
90
-
60
-
75
Чому
дорівнює розмірність ортогонального доповнення
![]() до підпростору
до підпростору
![]() , якщо
, якщо
![]() ?
?
-
2
-
3
-
1
-
0
Чому
дорівнює розмірність ортогонального доповнення
![]() до підпростору
до підпростору
![]() , якщо
, якщо
![]() ?
?
-
1
-
4
-
2
-
3
Чому
дорівнює розмірність ортогонального доповнення
![]() до підпростору
до підпростору
![]() , якщо
, якщо
![]() ?
?
-
4
-
3
-
2
-
1
Чому
дорівнює розмірність ортогонального доповнення
![]() до підпростору
до підпростору
![]() , якщо
, якщо
![]() ?
?
-
4
-
3
-
2
-
1
Лінійний
оператор
![]() векторного простору
векторного простору
![]() над полем дійсних чисел в деякому базисі
має матрицю
над полем дійсних чисел в деякому базисі
має матрицю
![]() . В якому
з вказаних випадків оператор
. В якому
з вказаних випадків оператор
![]() має
базис із власних векторів:
має
базис із власних векторів:
Нехай
![]() лінійний оператор
векторного простору
лінійний оператор
векторного простору
![]() . Яке з
вказаних тверджень є правильним:
. Яке з
вказаних тверджень є правильним:
-
якщо
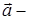 власний вектор
оператора
власний вектор
оператора
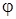 із власним
значенням
із власним
значенням
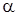 ,
,
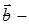 власний вектор
оператора
власний вектор
оператора
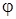 із власним
значенням
із власним
значенням
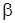 і
і
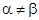 , то вектор
, то вектор
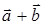 є власним вектором
оператора
є власним вектором
оператора
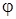 із власним
значенням
із власним
значенням
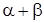
-
якщо
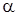 ,
,
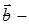 власні вектори
оператора
власні вектори
оператора
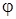 , які відповідають
власному значенню
, які відповідають
власному значенню
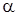 , то
, то
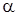 і
і
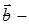 лінійно незалежні
лінійно незалежні
-
якщо
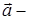 власний вектор
оператора
власний вектор
оператора
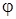 із власним
значенням
із власним
значенням
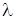 , то
, то
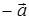 також є власним
вектором оператора
також є власним
вектором оператора
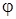 із
власним значенням
із
власним значенням
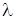
-
якщо
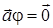 , то
, то
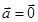
![]() ,
,
![]() . Який із даних
векторів є власним вектором оператора
. Який із даних
векторів є власним вектором оператора
![]() :
:
Який
з даних операторів
![]() векторного
простору є лінійним, якщо він заданий як функція координат вектора
векторного
простору є лінійним, якщо він заданий як функція координат вектора
![]() :
:
Білінійна
функція
![]() в деякому базисі
в деякому базисі
![]() двовимірного
простору
двовимірного
простору
![]() задано матрицею
задано матрицею
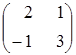 .
.
Знайти
![]() , якщо
, якщо
![]() ,
,
![]() .
.
-
5
-
2
-
6
-
-9
-
0
Білінійна
функція
![]() в деякому базисі
в деякому базисі
![]() тривимірного
простору
тривимірного
простору
![]() задано матрицею
задано матрицею
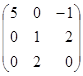 .
.
Знайти
![]() , якщо
, якщо
![]() ,
,
![]() .
.
-
5
-
3
-
4
-
-6
-
-12
Білінійна
функція
![]() в деякому базисі
в деякому базисі
![]() двовимірного
простору
двовимірного
простору
![]() задано матрицею
задано матрицею
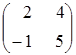 .
.
Знайти
![]() , якщо
, якщо
![]() ,
,
![]() .
.
-
5
-
29
-
-4
-
18
-
-6
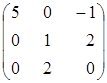 .
.
Знайти
![]() , якщо
, якщо
![]() ,
,
![]() .
.
-
9
-
2
-
-3
-
14
-
5
Яке з тверджень правильне:
-
сума розв’язку неоднорідної системи лінійних рівнянь і розв’язку відповідної однорідної системи рівнянь є розв’язком однорідної системи рівнянь
-
сума двох розв’язків однорідної системи лінійних рівнянь є розв’язком цієї системи
-
сума двох розв’язків неоднорідної системи лінійних рівнянь є розв’язком цієї системи рівнянь
-
сума двох розв’язків неоднорідної системи лінійних рівнянь є розв’язком відповідної однорідної системи рівнянь
Нехай
![]() – деяка матриця.
Яке з даних тверджень правильне:
– деяка матриця.
Яке з даних тверджень правильне:
-
сума стовпцевого і рядкового рангів матриці дорівнює нулю
-
різниця стовпцевого і рядкового рангів матриці дорівнює нулю
-
добуток стовпцевого і рядкового рангів матриці дорівнює нулю
-
частка стовпцевого і рядкового рангів матриці дорівнює нулю
Яке з даних тверджень для неоднорідної системи лінійних рівнянь є правильним:
-
якщо система сумісна, то вона визначена
-
якщо система невизначена, то вона несумісна
-
якщо система визначена, то вона сумісна
-
сумісна система завжди визначена
При
якому значенні
![]() ранг
матриці
ранг
матриці
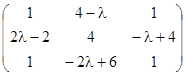 дорівнює 1?
дорівнює 1?
-
2
-
1
-
3
-
0
-
-1
Добуток
матриць
![]() існує, якщо
існує, якщо
-
матриці
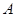 та
та
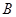 мають однакову
кількість стовпців
мають однакову
кількість стовпців
-
матриці
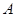 та
та
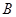 мають однакову
розмірність
мають однакову
розмірність
-
матриці
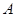 та
та
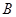 квадратні
квадратні
-
кількість стовпців у матриці
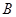 така ж як
кількість рядків у матриці
така ж як
кількість рядків у матриці
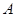
Знайти
детермінант добутку матриць
![]() і
і
![]() :
:
-
61
-
4
-
-6
-
-3
-
0
Знайти
детермінант добутку матриць
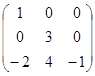 і
і
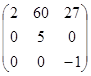 :
:
-
-2
-
4
-
36
-
18
-
30
Тема :: Математичний аналіз
- Жодна з вказаних вище.
- Добуток парної і непарної функцій є непарна функція
- Сума парної і непарної функцій є непарна функція.
- Добуток двох непарних функцій є непарна функція.
- опукла
- не обмежена
- приймає своє найбільше значення
- диференційовна
Обчислити найбільше значення функції
y
=
![]() 2
sin
(2
x
+1)
2
sin
(2
x
+1)
-
1
-
2
-
-1
-
4
Обчислити найменше значення функції y=6cos(13x+2)+4.
-
-1
-
-2
-
-4
-
2
Обчислити найбільше значення функції
y=
![]()
-
1
-
-3
-
3
-
5
-
0,5
-
0,75
-
1
-
0,657
З’ясувати, парна чи непарна функція
![]() якщо
якщо
![]() :
:
-
парна
-
непарна
-
ні парна, ні непарна
З’ясувати, парна чи непарна функція
![]() , якщо
, якщо
![]() , та вказати номер правильної
відповіді:
, та вказати номер правильної
відповіді:
-
парна
-
непарна
-
ні парна, ні непарна
З’ясувати, парна чи непарна функція
![]() , якщо
, якщо
![]() , та вказати номер
правильної відповіді:
, та вказати номер
правильної відповіді:
-
парна
-
непарна
-
ні парна, ні непарна
З’ясувати, парна чи непарна функція
![]() , якщо
, якщо
![]() :
:
-
парна
-
непарна
-
ні парна, ні непарна
Обчислити суму тих значень
х
, в
яких функція
![]() набуває
найменшого значення.
набуває
найменшого значення.
-
3
-
-2
-
-4
-
-3
Знайти
найменше із значень параметра
![]() , для яких
функція
, для яких
функція
![]() буде непарною.
буде непарною.
-
3
-
1
-
-2
-
-1
Обчислити
![]() , якщо
, якщо
![]()
-
576
-
577
-
582
-
575
Обчислити
![]() , якщо
, якщо
![]()
-
576
-
577
-
582
-
575
Обчислити
![]()
-
41
-
40
-
38
-
67
Обчислити
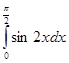
-
4
-
9
-
1
-
6
Обчислити
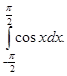
-
4
-
9
-
3
-
2
Обчислити
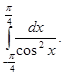
-
4
-
2
-
3
-
6
Обчислити
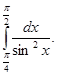
-
1
-
9
-
3
-
-1
Обчислити
![]()
-
1
-
9
-
4
-
6
Обчислити
![]()
-
4
-
1
-
3
-
6
Обчислити
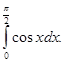
-
4
-
9
-
1
-
6
Обчислити
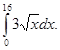
-
144
-
189
-
37
-
128
Обчислити
![]()
-
4
-
96.8
-
3
-
103
Обчислити
![]()
-
4
-
9
-
3
-
6
Обчислити
![]()
![]()
-
4
-
9
-
3
-
1
Обчислити
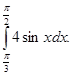
-
4
-
2
-
3
-
6
Обчислити
![]()
-
4
-
-2
-
2
-
6
Обчислити суму цілих значень
х
,
які входять в область визначення функції
![]() .
.
-
12
-
2
-
13
-
7
Обчислити суму тих значень
х
, в
яких функція
![]() набуває
найменшого значення.
набуває
найменшого значення.
-
3
-
-2
-
-4
-
-3
Обчислити
![]() , якщо
, якщо
![]()
-
-9
-
4
-
5
-
7
Обчислити
![]() , якщо
, якщо
![]()
-
8
-
1
-
14
-
-14
Обчислити
![]() , якщо
, якщо
![]()
-
5
-
11
-
15
-
5
Обчислити
![]() , якщо
, якщо
![]()
-
4
-
9
-
13
-
6
Обчислити
![]() , якщо
, якщо
![]()
-
6
-
9
-
13
-
-6
Обчислити
![]() , якщо
, якщо
![]()
-
4
-
9
-
7
-
6
Обчислити найбільше значення функції
![]() на проміжку
на проміжку
![]() .
.
-
8
-
9
-
13
-
6
Обчислити найменше значення функції
![]() на проміжку
на проміжку
![]() .
.
-
4
-
9
-
13
-
6
Скільки точок екстремуму має функція
![]() ?
?
-
4
-
3
-
2
-
1
Скільки точок екстремуму має функція
![]() ?
?
-
4
-
3
-
2
-
1
Обчислити
найменше значення функції
![]() на
проміжку
на
проміжку
![]() .
.
-
4
-
9
-
3
-
6
Обчислити
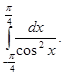
-
4
-
2
-
3
-
6
Обчислити
![]()
-
1.75
-
1.9
-
2.3
-
0.6
Знайти значення х, при якому значення
похідної функції
![]() дорівнює
нулю.
дорівнює
нулю.
-
0
-
2
-
0.13
-
-2
Обчислити
![]() , якщо
, якщо
![]()
-
1
-
4/3
-
15
-
-2
Обчислити
![]() , якщо
, якщо
![]()
-
0.2
-
4/3
-
1.5
-
0.5
Обчислити
![]() , якщо
, якщо
![]()
-
1
-
0.25
-
0.5
-
-0.5
Визначити
найменший додатний період функції y=2ctg(2
p
x+3)
![]() .
.
-
0.5
-
1
-
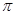
-
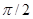
- збігається
- не обмежена зверху
- розбігається
- може як збігатись, так і розбігатись
- жодного
- 1
- 3
- нескінченно багато
- у деяких точках збігається, у деяких розбігається
- розбігається у кожній точці
- збігається умовно в кожній точці
- збігається абсолютно в кожній точці
- не спадає
- не зростає
- спадає
- зростає
- має нескінченну часткову границю
- має скінченну границю
- має часткову границю
- має нескінченну границю
- f(х) обмежена на (a; b)
- похідна функції f(х) в деякій точці перетворюється на 0 в інтервалі (a;b)
- f(х) монотонна на (a; b)
- f(х) неперервна на (a; b)
- розбігається
- може як збігатись, так і розбігатись
- не обмежена зверху
- збігається
- f(x) диференційовна
- f(x) розривна в точці х = 0
- f(0) = 0
- f(x) також парна на цьому відрізку
- f(х) неперервна на [a;b]
- f(х) неперервна на [a;b], за винятком скінченої кількості точок
- f(х) монотонна на [a;b]
- f(х) обмежена на [a;b]
- має скінченну або нескінченну границю
- збігається
- обмежена
- зростає
- має обернену функцію на [а, b]
- обмежена на [а, b]
- монотонна на [а, b]
- диференційовна на [а, b]
- вона має необмежену підпослідовність
- вона необмежена
- будь-яка її підпослідовність монотонна
- будь-яка її підпослідовність збігається
- монотонна на [а, b]
- обмежена на [а, b]
- неперервна на [а, b]
- диференційовна на інтервалі (c,d), що міститься в [а, b]
- Якщо послідовність обмежена і монотонна, то вона має границю.
- Якщо послідовність не має границі, то вона не є обмеженою.
- Якщо додатна послідовність прямує до нуля, то вона монотонна.
- Якщо послідовність обмежена, то вона має границю.
- має обернену функцію
- обмежена
- парна
- необмежена
- диференційовна
- обмежена
- неперервна
- має обернену функцію
- умовно збігається
- розбігається
- може як збігатись, так і розбігатись
- збігається
Тема :: Практикум розв’язування задач
Визначити суму коренів рівняння
![]()
-
5
-
3
-
8
-
4
Визначити суму коренів рівняння
![]() .
.
-
0.6
-
0.5
-
-0.8
-
-0.5
При якому значенні m рівняння 4х2 + mx - 1 = 0 має розв'язок х = 2?
-
-7.5
-
-5.4
-
-8.6
-
-7.8
При якому значенні
![]() рівняння
рівняння
![]() має розв’язок
має розв’язок
![]() ?
?
-
1
-
-5
-
3
-
-2
При якому значенні параметра
![]() сума коренів
рівняння
сума коренів
рівняння
![]() дорівнює 1?
дорівнює 1?
-
-0.5
-
1.2
-
0.5
-
0.8
При якому значенні параметра
![]() добуток коренів
рівняння
добуток коренів
рівняння
![]() дорівнює 6?
дорівнює 6?
-
-1.2
-
0.5
-
-1.6
-
1.2
-
4
-
1
-
2
-
6
Обчислити суму коренів рівняння
![]()
-
-4
-
3
-
-2
-
6
При якому значенні
![]() сума коренів
рівняння
сума коренів
рівняння
![]() дорівнює 4?
дорівнює 4?
-
-0.4
-
-0.8
-
0.5
-
-0.2
Визначити значення
![]() з пропорції
з пропорції
![]()
![]()
-
14
-
10
-
8
-
13
Обчислити
![]() , якщо (х, у) —
розв’язок системи
, якщо (х, у) —
розв’язок системи
![]()
-
2
-
3
-
8
-
5
Визначити абсцису точки перетину
прямих
![]() і
і
![]()
-
4
-
5
-
2
-
3
Визначити ординату точки перетину
прямих
![]() і
і
![]()
-
-3
-
-7
-
-4
-
-1
При якому значенні параметра a пряма aх - y + 9 = 0 проходить через точку A(-1; -3) ?
-
11
-
7
-
9
-
12
Знайти добуток координат точки
перетину прямих
![]()
-
-1
-
2
-
-3
-
5
Обчислити
![]() , якщо
, якщо
![]() — розв’язок системи
— розв’язок системи
![]()
-
4
-
1
-
2
-
6
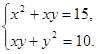
-
3
-
9
-
4
-
5
Обчислити
![]() , якщо
, якщо
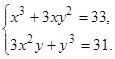
-
4
-
7
-
2
-
1
Обчислити
![]() , якщо
, якщо
![]() корені рівняння
корені рівняння
![]()
-
2
-
5
-
4
-
8
Обчислити добуток тих значень
параметра
![]() , при яких рівняння
, при яких рівняння
![]() має один корінь.
має один корінь.
-
-16
-
9
-
-9
-
-12
Обчислити
![]() , якщо
, якщо
![]() —
розв
’
язок системи
—
розв
’
язок системи
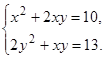
-
2
-
6
-
8
-
3
Обчислити
![]() , якщо
, якщо
![]() —
розв
’
язок системи
—
розв
’
язок системи
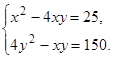
-
15
-
20
-
25
-
35
-
3
-
4
-
6
-
1
Скільки розв’язків має рівняння
![]() ?
?
-
1
-
5
-
4
-
2
Визначити суму коренів рівняння
![]() .
.
-
2
-
-3
-
4
-
-5
Скільки розв‘язків має рівняння
![]()
-
4
-
7
-
3
-
1
Розв‘язати рівняння
![]() .
.
-
2
-
4
-
7
-
5
Розв‘язати рівняння
![]() .
.
-
2
-
-6
-
-4
-
5
Знайти менший розв‘зок рівняння
![]()
-
2
-
-3
-
7
-
4
Обчислити
![]() якщо
якщо
![]()
-
6
-
2
-
9
-
4
Турист пройшов 40 % усього шляху. Залишилось пройти на 36 км більше, ніж пройшов. Яка довжина шляху (в кілометрах)?
-
165
-
180
-
192
-
184
Турист пройшов 1/4 шляху. Залишилось пройти на 24 км більше, ніж він пройшов. Яка довжина шляху ( в кілометрах )?
-
38
-
52
-
44
-
48
Турист пройшов 0,3 шляху. Залишилось пройти на 40 км більше, ніж він пройшов. Яка довжина шляху ( в кілометрах )?
-
100
-
84
-
112
-
96
Мати старша від дочки у 4 рази. Разом їм 35 років. Скільки років дочці?
-
7
-
5
-
9
-
8
Мати старша від дочки на 24 роки. Разом їм 44 роки. Скільки років матері?
-
37
-
32
-
34
-
42
Ціну товару збільшили на 62 % . У скільки разів став дорожчий товар?
-
1.48
-
1.62
-
1.75
-
1.84
Батько старший від сина в 2 рази. Скільки років синові, якщо батько старший на 20 років?
-
19
-
22
-
18
-
20
Батько старший від сина в 5 разів. Скільки років синові, якщо він молодший від батька на 20 років?
-
4
-
5
-
7
-
6
Гострі кути прямокутного трикутника відносяться як 8 : 1. Скільки градусів має менший гострий кут?
-
10
-
13
-
8
-
16
Сторони трикутника відносяться як 1 : 2 : 4. Обчислити довжину більшої сторони, якщо його периметр дорівнює 105.
-
52
-
48
-
60
-
64
Кути трикутника відносяться як 1 : 2 : 6. Скільки градусів має середній кут?
-
40
-
54
-
30
-
38
За два дні обробили 180 га пшениці, причому першого дня обробили на 12 га більше, ніж другого. Скільки гектарів обробили першого дня?
-
92
-
108
-
84
-
96
За два дні обробили 140 га пшениці, причому першого дня обробили на 26 га більше, ніж другого. Скільки гектарів обробили першого дня?
-
74
-
78
-
83
-
88
Два робітники виготовили разом 90 деталей, працюючи разом 9 днів. Скільки деталей за день виготовляв перший робітник, якщо другий виготовляв за день на 2 деталі менше?
-
6
-
8
-
5
-
9
Сума двох чисел дорівнює 15, а різниця їх дорівнює 11. Знайти більше із чисел.
-
15
-
14
-
13
-
16
Середнє геометричне двох чисел дорівнює 12. Знайти більше число, якщо менше дорівнює 6.
-
26
-
24
-
28
-
32
Сума двох чисел, одне із яких менше від другого на 7, дорівнює 53. Знайти менше число.
-
20
-
25
-
28
-
23
Середнє арифметичне двох чисел дорівнює 125, а більше із чисел дорівнює 126. Знайти менше число.
-
124
-
136
-
118
-
128
Двоє робітників разом виготовили 37 деталей. Перший виготовляв за день на 1 деталь більше від другого і працював 7 днів, а другий працював 8 днів. Скільки деталей за день виготовляв другий робітник?
-
3
-
5
-
2
-
4
В урні знаходиться 47 чорних і білих кульок. Якщо число чорних кульок зменшити на 11, то кульок стане порівну. Скільки чорних кульок в урні?
-
25
-
29
-
23
-
34
Фарфор складається з глини, піску і гіпсу, маси яких пропорційні числам 21, 4, 1. Скільки потрібно піску, щоб виготовити 780 кг суміші?
-
120
-
114
-
126
-
124
У двох хлопчиків 400 поштових марок. Якщо перший віддасть другому 20 марок, то в них марок стане порівну. Скільки марок у першого хлопчика?
-
226
-
244
-
220
-
212
На одній шальці терезів лежить кавун, а на другій – третина такого ж кавуна і гиря 4 кг. Терези перебувають у рівновазі. Яка маса кавуна?
-
7
-
11
-
8
-
6
Через три роки Галинка буде в 2 рази старша, ніж тепер. Скільки їй років тепер?
-
4
-
3
-
5
-
2
В одному бідоні в 3 рази більше молока, ніж у іншому. Якщо з першого бідона перелити 8 л молока в другий, то в обох бідонах молока стане порівну. Скільки молока було в першому бідоні?
-
28
-
19
-
24
-
22
Гострі кути прямокутного трикутника відносяться як 2:3. Скільки градусів має більший гострий кут?
-
54
-
39
-
48
-
62
Кути трикутника відносяться як 1:3:6. Скільки градусів має найбільший кут?
-
102
-
94
-
112
-
108
Середнє арифметичне двох чисел дорівнює 16, а менше з них дорівнює 14. Знайти більше число.
-
15
-
19
-
18
-
17
Сума двох чисел дорівнює 12, а різниця їх дорівнює 4. Знайти менше з цих чисел.
-
4
-
6
-
7
-
2
В урні знаходиться 38 чорних і білих кульок. Якщо число чорних кульок зменшити на 8, то кульок стане порівну. Скільки чорних кульок в урні?
-
21
-
23
-
18
-
26